Teorema Cavalierly

PEMBUKTIAN VOLUME BOLA

Dengan TEOREMA CAVALIERLY

Bonaventura Fransesco Cavalieri (1598-1647) adalah murid Galileo. Bukunya yang paling berpengaruh, Geometria Indivisibilibus Continuorum Nova ratione promota quadam, telah selesai pada 1629 dan diterbitkan pada 1635. Kutipan berikut, yang dikenal sebagai Teorema Cavalieri  atau Prinsip Cavalieri, diambil dari Buku VII, Teorema 1, Proposisi 1. 

Cavalierly Theorem : “If between the same parallels any two plane figures are constructed and if in them, any straight lines being drawn equidistant from the parallels, the included portions of any one of these lines are equal, the plane figures are also equal to one another; and if between the same parallel planes any solid figures are constructed and if in them, any planes being drawn equidistant from the parallel planes, the included plane figures out of any one of the planes so drawn are equal, the solid figures are likewise equal to one another”.

Misalkan volume kerucut adalah 1/3 x Luas Alas x Tinggi dan menggunakan prinsip Cavalierli, maka akan ditunjukkan bahwa Volume bola adalah 4/3 x π x r³.

• Bukti  :

Misalkan diberikan sebuah tabung dengan jari-jari alasnya adalah r cm dan tingginya adalah r cm dan sebuah benda setengah bola dengan jari-jarinya adalah r cm. Perhatikan daerah yang diarsir pada masing-masing dibawah ini.

                
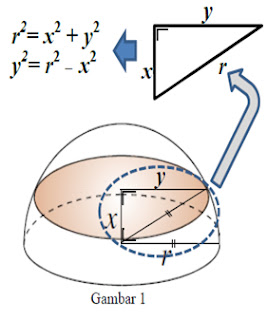
Perhatikan daerah yang diarsir pada gambar 1, luas daerah tersebut berbentuk lingkaran dengan jari-jarinya y cm. Dengan menggunakan teorema phytagoras, maka diperoleh y² = r² – x² sehingga luas daerah lingkaran tersebut (A1) menjadi πy² = π(r² – x² ) = πr² – πx². Dilain pihak, luas daerah pada gambar 2 yaitu berupa daerah cakram berlubang atau secara analitis dapat diuraikan menjadi luas daerah lingkaran (dengan jari-jarinya r) – luas daerah lingkaran (dengan jari-jarinya x) yaitu πr² – πx². Dengan demikian, luas daerah pada gambar 1 dan 2 adalah sama. Lebih lanjut, karena tinggi masing-masing benda sama yaitu r cm, maka berdasarkan teorema Cavalierly diperoleh volume masing-masing benda adalah sama. 

Perhatikan volume benda diluar kerucut (V₃) pada gambar 2, sehingga diperoleh V₃= volume tabung – volume kerucut = πr²t – 1/3 πr²t = πr²r - 1/3πr²r = πr³ - 1/3 πr³ = 2/3 πr³. Hal ini berarti, volume setengah bola yaitu 2/3 πr³ cm³ atau dengan kata lain volume bola tersebut adalah 2 x 2/3 πr³ cm³ = 4/3 πr³ cm³.

Sumber :

http://discreteteaching.com/3-4-dimensions.pdf;

http://www2.edc.org/mathproblems/problems/printProblems/ekvolrev2.pdf;

http://public.csusm.edu/aitken_html/m330/CavPrinciple.pdf;

http://kr.cs.ait. ac.th/~radok/math/mat2/chap89.html